This is default featured slide 1 title
Go to Blogger edit html and find these sentences.Now replace these sentences with your own descriptions.
This is default featured slide 2 title
Go to Blogger edit html and find these sentences.Now replace these sentences with your own descriptions.
This is default featured slide 3 title
Go to Blogger edit html and find these sentences.Now replace these sentences with your own descriptions.
This is default featured slide 4 title
Go to Blogger edit html and find these sentences.Now replace these sentences with your own descriptions.
This is default featured slide 5 title
Go to Blogger edit html and find these sentences.Now replace these sentences with your own descriptions.
9.5.10
integrales indefinidas
Material proporcionado por la Lic. Elizabeth Igarza Campos, encargada del curso matematica para economistas de la escuela de Economia de la UNSM
integrales indefinidas
integrales indefinidas
6.5.10
Integrales Impropias
Las denominadas integrales impropias son una clase especial de integrales definidas (integrales de Riemann) en las que el intervalo de integración o la función en el integrando o ambos presentan ciertas particularidades. Las integrales impropias no son realmente una nueva forma de integrales, sino una extensión natural a las propiedades de la integral y un replanteamiento de nuestro concepto de área bajo la curva.
 es impropia si se presenta uno de los siguientes casos:
es impropia si se presenta uno de los siguientes casos:1.- a = -  o b =
o b =  a = -
a = -  y b =
y b = 
 o b =
o b =  a = -
a = -  y b =
y b = 
2.-  no es acotada en alguno de los puntos de
no es acotada en alguno de los puntos de  dichos puntos se llaman singularidades de
dichos puntos se llaman singularidades de 
 no es acotada en alguno de los puntos de
no es acotada en alguno de los puntos de  dichos puntos se llaman singularidades de
dichos puntos se llaman singularidades de 
Existes diversos tipos de integrales impropias las cuales definiremos a continuación:







Cuando los límites, en las definiciones anteriores, existen, se dice que la integral es convergente, en caso contrario, se dice que la integral es divergente.
Principales definiciones y teoremas
Definición 1 Sea una función integrable Riemann en cualquier intervalo
integrable Riemann en cualquier intervalo ![$[a,t]\subset[a,b)$](http://euler.us.es/%7Erenato/clases/programa/img308.png) . Si existe el límite
. Si existe el límite

diremos que existe la integral impropia en
en  que converge a
que converge a  y escribiremos
y escribiremos

Si no existe el anterior diremos que la integral impropia
anterior diremos que la integral impropia  diverge.
diverge.
Análogamente se pueden definir las integrales impropias en![$(-\infty,a]$](http://euler.us.es/%7Erenato/clases/programa/img314.png) .
.
Definición 2 Sea una función integrable en cualquier intervalo
una función integrable en cualquier intervalo ![$[a,t]\subset[a,b)$](http://euler.us.es/%7Erenato/clases/programa/img308.png) ,
,  . Si existe el límite
. Si existe el límite

diremos que existe la integral impropia de segunda especie en
en  que converge a
que converge a  y escribiremos
y escribiremos

Si no existe el anterior diremos que la integral impropia
anterior diremos que la integral impropia  diverge. Observación: Obviamente ambas definiciones se pueden unificar en una única
diverge. Observación: Obviamente ambas definiciones se pueden unificar en una única
Definición 3 Sea una función integrable Riemann en cualquier intervalo
integrable Riemann en cualquier intervalo ![$[a,t]\subset[a,b)$](http://euler.us.es/%7Erenato/clases/programa/img308.png) . Si existe el límite
. Si existe el límite

diremos que existe la integral impropia en
en  que converge a
que converge a  y escribiremos
y escribiremos

Si no existe el anterior diremos que la integral impropia
anterior diremos que la integral impropia  diverge.
diverge.
Teorema 1 Criterio de comparación para las integrales impropias. Sean y
y  dos funciones integrables en cualquier intervalo
dos funciones integrables en cualquier intervalo ![$[a,t]\subset[a,b)$](http://euler.us.es/%7Erenato/clases/programa/img308.png) tales que
tales que

Entonces si la integral es convergente, la integral
es convergente, la integral  también lo es, y si
también lo es, y si  es divergente, entonces
es divergente, entonces  también será divergente.
también será divergente.
Teorema 2 Criterio de Abel-Dirichlet para las integrales impropias.
Sean y
y  dos funciones integrables en cualquier intervalo
dos funciones integrables en cualquier intervalo ![$[a,t]\subset[a,b)$](http://euler.us.es/%7Erenato/clases/programa/img308.png) y sea
y sea  una función monótona. Entonces, para que la integral impropia
una función monótona. Entonces, para que la integral impropia  converja es suficiente que se cumplan cualquiera de las dos siguientes pares de condiciones:
converja es suficiente que se cumplan cualquiera de las dos siguientes pares de condiciones:
a) converja y
converja y  acotada en
acotada en  , o
, o
b) este acotada para todo
este acotada para todo  y
y  converja a cero cuando
converja a cero cuando  .
.
Algunos ejemplos resueltos:


La integral converge a 1.


La integral converge a



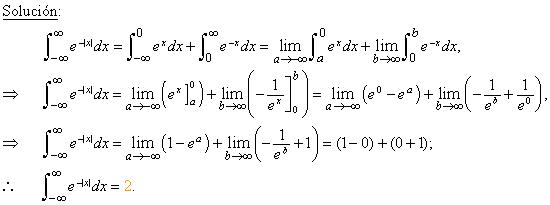
La integral converge a 2.


La integral converge a
Aquí algunos vodeos respecto a nuestro tema:
Definición 1 Sea una función
diremos que existe la integral impropia
 en
en Si no existe el
 diverge.
diverge.Análogamente se pueden definir las integrales impropias en
Definición 2 Sea
diremos que existe la integral impropia de segunda especie
 en
en Si no existe el
 diverge. Observación: Obviamente ambas definiciones se pueden unificar en una única
diverge. Observación: Obviamente ambas definiciones se pueden unificar en una única Definición 3 Sea una función
diremos que existe la integral impropia
 en
en Si no existe el
 diverge.
diverge. Teorema 1 Criterio de comparación para las integrales impropias. Sean
Entonces si la integral
 es convergente, la integral
es convergente, la integral  también lo es, y si
también lo es, y si  es divergente, entonces
es divergente, entonces  también será divergente.
también será divergente. Teorema 2 Criterio de Abel-Dirichlet para las integrales impropias.
Sean
 converja es suficiente que se cumplan cualquiera de las dos siguientes pares de condiciones:
converja es suficiente que se cumplan cualquiera de las dos siguientes pares de condiciones: a)
 converja y
converja y b)
 este acotada para todo
este acotada para todo Algunos ejemplos resueltos:


La integral converge a 1.


La integral converge a




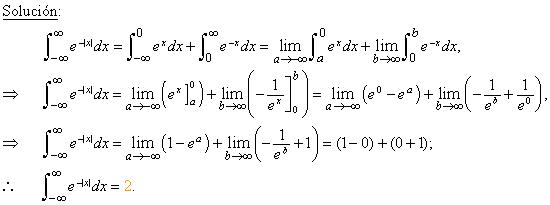
La integral converge a 2.


La integral converge a

Aquí algunos vodeos respecto a nuestro tema:










